تحلیل واریانس یک راهه (ANOVA) یکی از تحلیل‌های پرکاربرد است که در تمامی علوم کاربرد دارد. به زبان ساده می‌توان چنین گفت که اگر شما دو یا بیش از دو گروه داشته باشید و بخواهید نمره یک متغیر را در این گروه‌ها مقایسه کنید باید از این آزمون استفاده کنید. فرض کنید که نمره سن سه گروه کارشناسی، کارشناسی ارشد و دکتری  را در دست داریم و می‌خواهیم ببینیم که آیا تفاوتی در سن این سه گروه وجود دارد یا خیر. در این صورت از تحلیل واریانس یک راهه (ANOVA) استفاده می‌کنیم. اگر دو گروه داشته باشیم هم می‌توانیم از تحلیل واریانس یک راهه استفاده کنیم و هم تحلیل t مستقل.

پیشفرض‌های تحلیل واریانس یک راهه (ANOVA)

۱- متغیر وابسته شما (در اینجا سن) باید در سطح فاصله‌ای یا نسبی باشد.

۲- متغیر مستقل (در اینجا گروه دانشگاهی) باید اسمی یا رتبه‌ای باشد.

۳- توزیع داده‌های متغیر وابسته باید به صورت نرمال باشد (تحلیل کولموگروف – اسمیرنوف).

اجرای آموزش تحلیل واریانس یک راهه (ANOVA) در SPSS

نرم افزار SPSS را باز کرده و به مسیر زیر بروید: Analyze> Compare Means> One Way Anova.

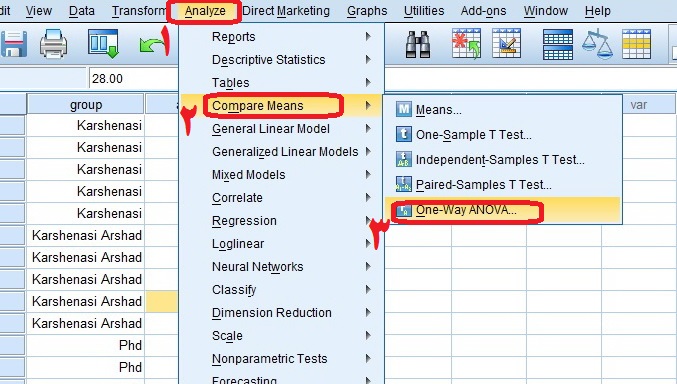
پس از باز شدن صفحه جدید، مطابق شکل زیر متغیر وابسته (سن) را در کادر Dependent List وارد کنید و در کادرFactor متغیر گروه را وارد کنید. در مرحله بعد گزینه Post Hoc را بزنید.

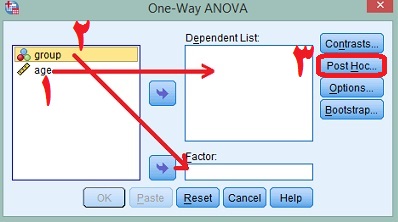در صفحه جدید تیک گزینه Scheffe را بزنید تا تحلیل تعقیبی شفه انتخاب شود سپس بر روی گزینه Continue  کلیک کنیدو پس از آن Ok را کلیک کنید. دلیل انتخاب این گزینه به سبب وجود سه گروه است. تحلیل واریانس یک راهه دو جدول به شما خواهد داد. در جدول اول نشان داده می‌شود که آیا بین این سه گروه تفاوت وجود دارد یا نه. فرض کنید که تفاوت معناداری مشاهده شد، در این صورت ما نمی‌دانیم که کدام گروه با کدام گروه دیگر تفاوت دارد. آیا سن کارشناسی از کارشناسی ارشد کمتر است؟ آیا سن کارشناسی از دکتری کمتر است؟ آیا سن کارشناسی ارشد از دکتری کمتر است؟ در واقع جدول اول پاسخ این سوالات را به شما نمی‌دهد و فقط بیان می‌کند که تفاوت وجود دارد. اما تحلیل تعقیبی شفه نشان می‌دهد که تفاوت مشاهده شده بین کدام گروه است.

در مرحله بعد نتایج خروجی SPSS مشاهده می‌گردد. در این جدول دو شاخص F و Sig مهم هستند. اگر Sig کمتر از ۵ صدم باشد به معنی این است که بین گروه‌ها تفاوت معناداری وجود دارد که در جدول زیر نیز این تفاوت دیده می‌شود.

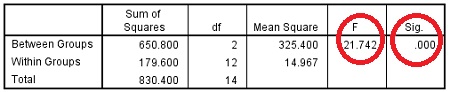
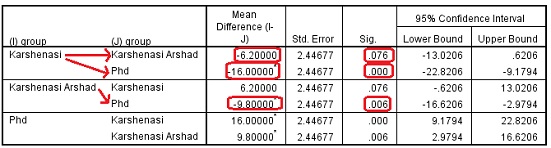
در جدول شماره بعدی نتایج تحلیل تعقیبی مشاهده می‌شود.در این جدول نتایج سه گروه به تفکیک آمده است. برای مثال در سطر اول مشاهده می‌شود که دانشجویان کارشناسی ۶ نمره از دانشجویان کارشناسی ارشد سن پایین‌تری دارند اما این تفاوت معنادار نیست درحالی که میان سن کارشناسی و دکتری و کارشناسی ارشد و دکتری تفاوت معناداری وجود دارد.