در حدود سال 1930 به مطالعه یک نوع ضریب همبستگی پرداخت که به نام او شهرت دارد. در سال 1948 رساله ای در این باره منتشر کرد که محتوی تئوری این ضریب همبستگی می باشد.در آمار، ضریب همبستگی رتبهای کندال که به تای کندال مشهور است و با حرف یونانی τ نمایش داده میشود یک آماره ی ناپارامتری است که برای سنجش همبستگی آماری میان دو متغیر تصادفی به کار میرود.

خواص ضریب همبستگی کندال
- از آنجایی که مخرج این کسر تعداد انتخابهای زوجها از بین n مشاهده است، همیشه از صورت بزرگتر است. پس ضریب همبستگی کندال از 1 کوچکتر و از 1- بزرگتر است.
- اگر همه زوجها با هم هماهنگ باشند مقدار ضریب همبستگی کندال برابر است با 1.
- اگر همه زوجها ناهماهنگ باشند ضریب همبستگی کندال برابر است با 1-.
- اگر X و Y مستقل باشند، انتظار داریم که ضریب همبستگی کندال نیز برابر با ۰ باشد.
فرمول محاسبه ضریب همبستگی کندال
T=2Sn(n−1)T=2Sn(n-1)
در فرمول فوق n حجم نمونه مورد بررسی می باشد.مقدار S از مجموع اختلاف ui (تعداد داده هایی که بعد از داده ی مورد نظر قرار گرفته و بیشتر از آن است) و vi (تعداد داده هایی که بعد از داده ی مورد نظر قرار گرفته و کمتر از آن است) بدست می آید :
S=∑i=1ndi=∑i=1n(ui−vi)S=∑i=1ndi=∑i=1n(ui-vi)
حل مثال دستی ضریب همبستگی Kendall
در جدول زیر نمرات امتحان x و y ده دانش آموز ثبت شده است با استفاده از ضریب همبستگی کندال رابطه بین دو امتحان را محاسبه کنید :
| 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | دانش آموز |
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 1 | 6 | 4 | 10 | 7 | 2 | 9 | 3 | 8 | نمره امتحان x |
| 6 | 2 | 4 | 3 | 7 | 8 | 1 | 5 | 10 | 9 | نمره امتحان y |
برای بدست آوردن ضریب همبستگی کندال ابتدا نمرات امتحان x را از کوچک به بزرگ مرتب به صورت زیر مرتب می کنیم و نمرات امتحان y را متقابلا در جدول یادداشت می نماییم :
| 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | دانش آموز |
|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | نمره امتحان x |
| 7 | 10 | 9 | 8 | 4 | 6 | 3 | 5 | 1 | 2 | نمره امتحان y |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 2 | 0 | 1 | vi |
| 0 | 0 | 1 | 2 | 4 | 4 | 6 | 4 | 8 | 8 | ui |
| 0 | 1- | 0 | 1 | 4 | 4 | 6 | 2 | 8 | 7 | di |
محاسبه زوج های هماهنگ و ناهماهنگ
طریقه محاسبه vi بدین صورت است : نمره امتحان y دانش آموز اول را بررسی کرده (برابر 2 است) و به تعدادی که در نمرات سمت راستش کوچکتر از 2 مشاهده کردیم مقدار ui مشخص می شود (در امتحان y فقط نمره دانش آموز دوم از دانش آموز اول کمتر است) پس مقدار 1 اختیار می کند. برای دانش آموز دوم نیز که نمره امتحان y آن برابر 1 است مشاهده می شود که هیچکدام از دانش آموزان بعدی نمره کمتری از او نگرفته اند، لذا مقدار vi برای دانش آموز دوم برابر صفر می باشد.
طریقه محاسبه ui بدین صورت است : نمره امتحان y دانش آموز اول را بررسی کرده (برابر 2 است) و به تعدادی که در نمرات سمت راستش بزرگتر از 2 مشاهده کردیم مقدار vi مشخص می شود (در امتحان y فقط نمره دانش آموز دوم از دانش آموز اول کمتر است) پس مقدار 8 اختیار می کند (اگر بشماریم نمره y دانش آموز اول از 8 دانش آموز بعدی کمتر است). برای دانش آموز دوم نیز که نمره امتحان y آن برابر 1 است مشاهده می شود که هیچکدام از دانش آموزان بعدی نمره کمتری از او نگرفته اند، لذا مقدار vi برای دانش آموز دوم نیز برابر 8 می باشد (فقط نمرات دانش آموزان سمت راست باقی مانده را در شمارش به حساب می آوریم). در انتها مقدار S به صورت زیر بدست می آید :
S=∑i=110di=∑i=110(ui−vi)=31S=∑i=110di=∑i=110(ui-vi)=31
T=2Sn(n−1)=2⋅3110(9−1)=0.689T=2Sn(n-1)=2⋅3110(9-1)=0.689
حل مثال همبستگی کندال در SPSS
ابتدا به شکل زیر داده ها را وارد نرم افزار SPSS می کنیم : برای دریافت آموزش نحوه ورود داده ها در نرم افزار SPSS اینجا کلیک کنید.
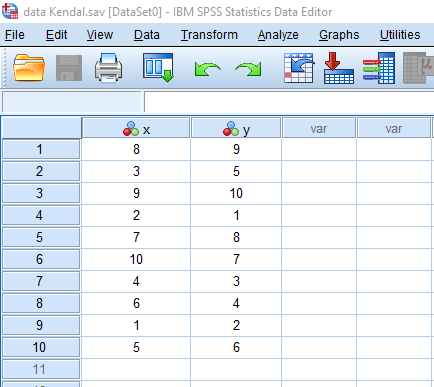
سپس از طریق دستور زیر کادر آزمون ضریب همبستگی میان دو متغیر را باز می کنیم :
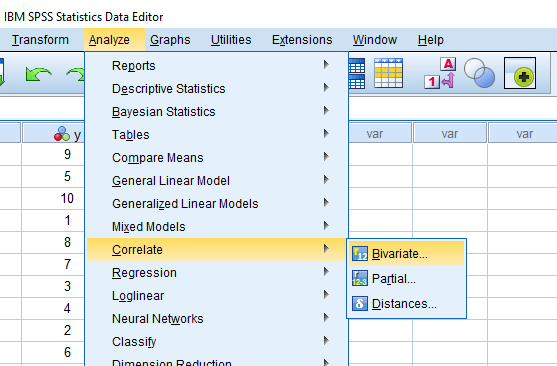
مانند شکل زیر در پنجره باز شده دو متغیر مورد نظر را وارد کادر Variables کنید و تیک ضریب همبستگی تاو-کندال را فعال نمایید، در انتها بر روی گزینه OK کلیک نمایید :
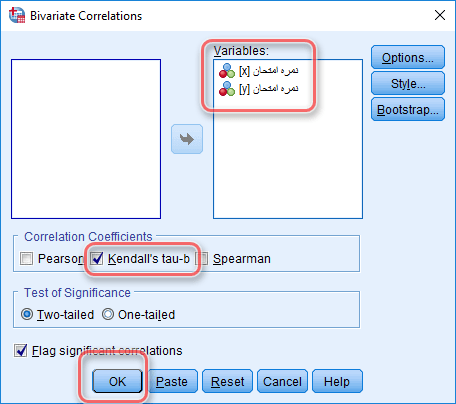
خروجی نرم افزار SPSS برای ضریب همبستگی کندال (KENDALL CORRELATION COEFFICIENTS) به صورت زیر است :
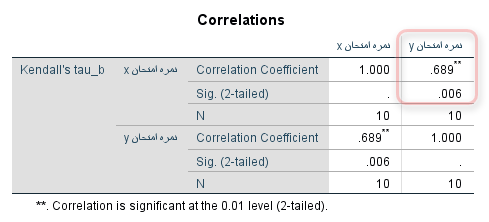
همانطور که مشاهده می شود مقدار ضریب همبستگی برابر با 0.689 بدست آمده است که سطح معنی داری آن با توجه به این که کمتر از 0.05 است نشان از معنی داری این ضریب می باشد.
عالی بود ممنون
سپاس از شما دوست گرامی
واقعا ممنون بخاطر سایت خوبتون. توضیحات کاملی بود. خودم آزمون ضریب همبستگیم رو انجام دادم. ممنون